نحوه محاسبه محیط مساحت مثلث + شکل و مثال

شاید این مطالب برایتان مفید باشد

حروف الفبا به ترتیب | شعر، جدول و آموزش

3 هفته پیش

معرفی میخکوبی و نقش آن در ساخت و ساز

3 هفته پیش

مشاوره انتخاب رشته در کنکور

7 فروردین, 1403

محیط: به زبان ساده، دور تا دور هر شکلی محیط آن است. در توضیحی جامع تر محیط به مجموع مسافتی که پیرامون شکل های هندسی به خط و مسیری گفته می شود که یک سطح را در بر می گیرد و برحسب متر محاسبه می شود.

مساحت: یک محدوده، با توجه به شکل و اندازه درونی شکل‌های دوبعدی و سطح بیرونی اشکال هندسی است، که برحسب متر مربع محاسبه می شود.

در این مقاله با ما همراه باشید، تا با نحوه محاسبه محیط و مساحت مثلث همراه شکل و مثال های برای آن ها بیشتر آشنا شوید.

نحوه محاسبه محیط مثلث

با استفاده از خط کش، طول هر ضلع مثلث را اندازه‌گیری می کنیم و عدد آن را در کنار ضلع مثلث. می نویسیم که محیط مثلث چقدر است؟ در انتها اندازه هر ضلع آن را با یکدیگر جمع میکنیم. بنابراین به راحتی محیط مثلث محاسبه می شود.

فرومل محیط مثلث: ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

محاسبه محیط مثلث به همراه مثال:

 

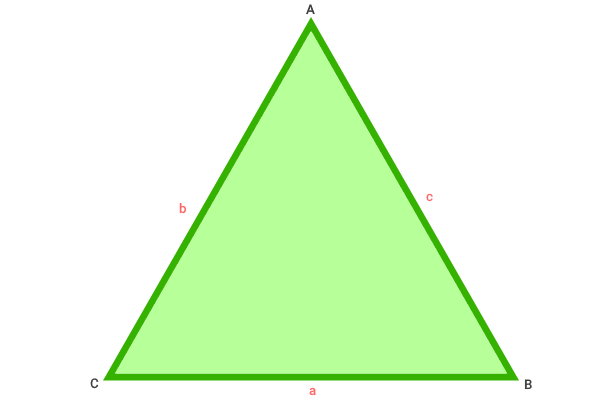
مطابق با تعریف، محیط مثلث از جمع اندازه ضلع‌های آن به دست می‌آید. این تعریف را می‌توان به صورت فرمول زیر نوشت:

$$P=a+b+c$$

• P: محیط مثلث ABC
• a: اندازه ضلع BC
• b: اندازه ضلع AC
• c: اندازه ضلع AB

تصویر زیر، یک مثلث متساوی الساقین و اندازه دو ضلع آن را نمایش می‌دهد. اگر محیط این مثلث برابر 25 سانتی‌متر باشد، اندازه ضلع سوم آن چند سانتی‌متر است؟

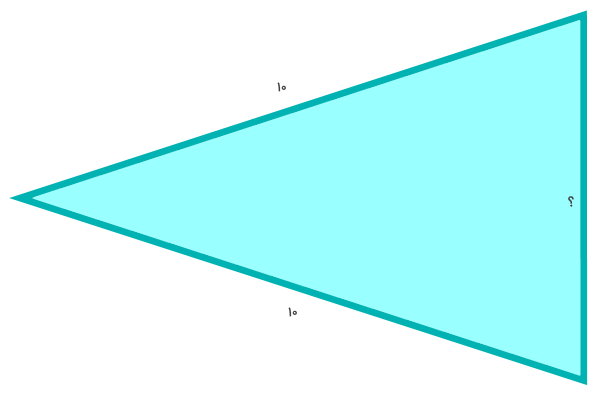
فرمول محیط مثلث (تمام انواع مثلث)، برابر است با:

$$P=a+b+c$$

• P: محیط مثلث برابر 25
• a: اندازه ضلع اول برابر 10
• b: اندازه ضلع دوم برابر 10
• c: اندازه ضلع سوم

اگر اندازه‌های معلوم را در فرمول بالا قرار دهیم و آن را بر حسب c حل کنیم، اندازه ضلع سوم مثلث متساوی الساقین به دست می‌آید:

$$25=10+10+c$$

$$25=20+c$$

$$c=25-20$$

$$c=5$$

اندازه ضلع سوم مثلث برابر 5 سانتی‌متر است.

محیط هر یک از مثلث‌های متساوی الاضلاع زیر را به دست بیاورید. اندازه محیط‌ها را با هم مقایسه کنید. آیا رابطه‌ای بین محیط‌های مثلث‌های متساوی الاضلاع وجود دارد؟

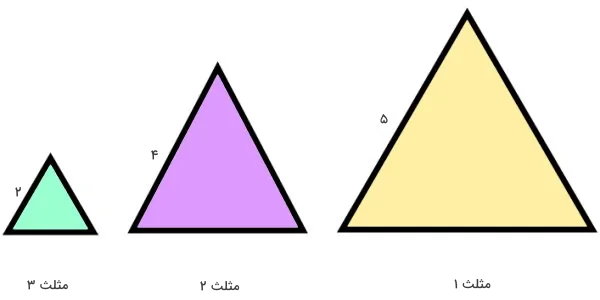
هر سه مثلث بالا، متساوی الاضلاع هستند. محاسبات را نوشتن فرمول محیط مثلث متساوی الاضلاع برای مثلث ۱ شروع می‌کنیم:

$$P_1=3a_1$$

• P₁: محیط مثلث متساوی الاضلاع 1
• a₁: اندازه ضلع مثلث متساوی الاضلاع 1 برابر 5

$$P_1=3\times 5$$

$$P_1=15$$

فرمول محیط مثلث ۲ به صورت زیر نوشته می‌شود:

$$P_2=3a_2$$

• P₂: محیط مثلث متساوی الاضلاع 2
• a₂: اندازه ضلع مثلث متساوی الاضلاع 2 برابر 4

$$P_2=3\times 4$$

$$P_2=12$$

فرمول محیط مثلث ۳ نیز برابر است با:

$$P_3=3a_3$$

• P₂: محیط مثلث متساوی الاضلاع 3
• a₂: اندازه ضلع مثلث متساوی الاضلاع 3 برابر 2

$$P_3=3\times 2$$

$$P_3=6$$

برای مقایسه مثلث‌ها، نسبت محیط آن‌ها را تعیین می‌کنیم:

$$\frac{P_1}{P_2}=\frac{15}{12}=\frac{5}{4}$$

$$\frac{P_1}{P_3}=\frac{15}{6}=\frac{5}{2}$$

$$\frac{P_2}{P_3}=\frac{12}{6}=2$$

نسب اندازه ضلع‌ها را هم می‌نویسیم:

$$\frac{a_1}{a_2}=\frac{5}{4}$$

$$\frac{a_1}{a_3}=\frac{5}{2}$$

$$\frac{a_2}{a_3}=\frac{4}{2}=2$$

همان طور که مشاهده می‌کنید، نسب محیط مثلث‌های متساوی الاضلاع، همان نسبت اندازه ضلع‌های آن‌ها است.

نحوه محاسبه مساحت مثلث

برای محاسبه ی مساحت مثلث، باید ابتدا ارتفاع مثلث را در قاعده آن ضرب کرده سپس تقسیم بر 2 کنیم تا مساحت مثلث را بدست آوریم.

فرمول مساحت مثلث: ۲ ÷ (ارتفاع  قاعده) = مساحت مثلث

محاسبه مساحت مثلث به همراه مثال:

تصویر زیر را در نظر بگیرید. اگر پاره خط (الف ث)، ارتفاع مثلث و ضلع (ب پ)، قاعده‌ی نظیر آن باشد. با توجه به اعداد نمایش داده شده در تصویر، مساحت مثلث چقدر است؟

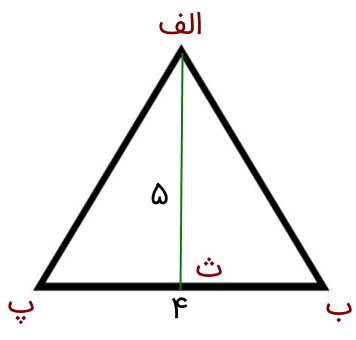
مثال ساده محاسبه مساحت مثلث

فرمول مساحت مثلث برابر است با:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

با توجه به اطلاعات سوال، داریم:

• قاعده = ضلع (ب پ) = 4
• ارتفاع = پاره خط (الف ث) = 5

اعداد بالا را درون فرمول مساحت مثلث‌ها قرار می‌دهیم:

۲ ÷ (پاره خط الف ث $$\times$$ ضلع ب پ) = مساحت مثلث (الف ب پ)

۲ ÷ (5$$\times$$4) = مساحت مثلث (الف ب پ)

۲ ÷ (20) = مساحت مثلث (الف ب پ)

10 = مساحت مثلث (الف ب پ)

به این ترتیب، سطح مثلث (الف ب پ) برابر با 5 خواهد بود. فرمول قاعده ضربدر ارتفاع تقسیم بر دو، برای اندازه‌گیری مساحت تمام انواع مثلث‌ها قابل استفاده است. با این وجود، فقط اگر ارتفاع و قاعده مثلث مشخص باشند می‌توان از این فرمول استفاده کرد. در بخش‌های بعدی، مثال‌های بیشتری را با استفاده از این فرمول حل خواهیم کرد.

مساحت سه مثلث نمایش داده شده در تصویر زیر را حساب کنید.

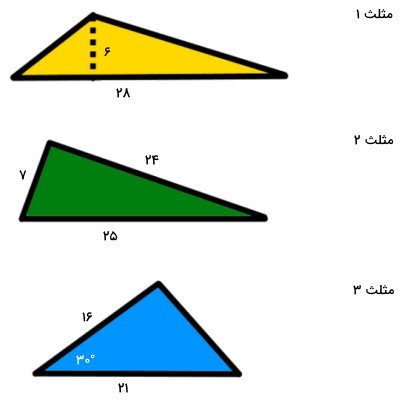
برای مثلث شماره 1، اندازه‌های قاعده و ارتفاع نظیر مثلث داده شده‌اند. بنابراین، فرمول مناسب برای محاسبه مساحت این مثلث، عبارت است از:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$A=\frac{h\times b}{2}$$

• A₁: مساحت مثلث شماره ۱
• b: قاعده برابر 28
• h: ارتفاع برابر 6

اندازه‌های معلوم را درون فرمول قرار می‌هیم و مقدار مساحت مثلث شماره 1 را محاسبه می‌کنیم:

$$A=\frac{6\times 28}{2}$$

$$A=3\times 28$$

$$A=84$$

مساحت مثلث شماره 1 برابر 84 است. در ادامه، مساحت مثلث شماره 2 را به دست می‌آوریم. اندازه‌های هر سه ضلع این مثلث معلوم و متفاوت هستند. در نتیجه، استفاده از فرمول هرون، بهترین گزینه برای محاسبه مساحت است. این فرمول را به همراه اندازه هر ضلع یادداشت می‌کنیم:

$$A=\sqrt{s(s-a)(s-b)(s-c)}$$

• A₂: مساحت مثلث شماره ۲
• a: اندازه ضلع a برابر 7
• b: اندازه ضلع b برابر 25
• c: اندازه ضلع c برابر 24

نصف محیط مثلث، عبارت است از:

$$s=\frac{7+25+24}{2}$$

$$s=\frac{56}{2}$$

$$s=28$$

نصف محیط را به همراه دیگر اندازه‌های معلوم، درون فرمول هرون قرار می‌هیم:

$$A=\sqrt{28(28-7)(28-25)(28-24)}$$

$$A=\sqrt{28\left(21\right)\left(3\right)\left(4\right)}$$

$$A=\sqrt{7056}$$

$$A=84$$

مساحت مثلث شماره ۲ نیز برابر 84 است. همان طور که مشاهده می‌کنید، با وجود اندازه‌های متفاوت، مساحت‌های دو مثلث 1 و 2 برابر هستند. در مثلث سوم، اندازه دو ضلع و زاویه بین آن‌ها داده شده است. برای محاسبه مساحت این مثلث، فرمول زیر را می‌نویسیم:

$$A=\frac{1}{2}a\cdot b\cdot sinC$$

• A₃: مساحت مثلث شماره ۳
• a: اندازه ضلع اول برابر 16
• b: اندازه ضلع دوم برابر 21
• C: زاویه بین اضلاع اول و دوم برابر 30 درجه

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$A=\frac{1}{2}\times 16\times 21\times \sin 30°$$

$$A=8\times 21\times 0.5$$

$$A=4\times 21$$

$$A=84$$

مساحت مثلث شماره ۳ نیز مانند مثلث‌های ۱ و ۲ برابر 84 است. به منظور محاسبه مساحت برای مثلث‌های معرفی شده در این مثال، تمام اندازه‌های مورد نیاز داده شده بود. اگر حتی یکی از این اندازه‌ها مشخص نبود، امکان تعیین مساحت وجود نداشت. با این وجود، در مثلث‌های خاص، نیازی به دانستن تمام انداز‌ه‌ها نیست. به عنوان مثال، مساحت مثلث متساوی الاضلاع، فقط با داشتن اندازه یکی از ضلع‌ها یا اندازه یکی از ارتفاع‌ها به دست می‌آید.