دانشنامه سیب دانشنامه سیب ! دکوراسیون داخلی، پزشکی و زندگی روزمره
شاید این مطالب برایتان مفید باشد
ذوزنقه یک شکل هندسی جالب و با ویژگیهای منحصر به فرد است. این ویژگیها به طور خلاصه در زیر توضیح داده شدهاند:
- زوایای مکمل: زوایای مجاور به هر ساق در ذوزنقه، به یکدیگر مکمل هستند، به این معنا که جمع اندازه زاویهای که به هر ساق وصل میشود و زاویه مجاور به آن ساق برابر ۱۸۰ درجه است.
- ساقهای متساوی طول: دو ساق شکل در ذوزنقه که از مجموع ۴ ساق تشکیل شدهاند، همواره برابر هستند. این ویژگی آن را به نام ذوزنقه متساوی الساقین معروف کرده است.
- زوایای مجاور متساوی: زوایای مجاور به هر قاعده (ضلع موازی به ساقهای موازی) در ذوزنقه، با یکدیگر برابرند، به عبارت دیگر زواج میان زاویههای مجاور برابر است.
- قطرهای مساوی: قطرهای ذوزنقه با یکدیگر برابرند. قطر از یک نقطه بر خلافی به نقطه مقابل روی شکل میرسد. این ویژگی نشان میدهد که از نظر اندازه، ذوزنقه تقریبا به اشکال مربعی نزدیک است.
- ذوزنقه قائمالزاویه: ذوزنقهای که یکی از زوایایش قائم است، به عنوان ذوزنقه قائمالزاویه شناخته میشود. در این حالت، یکی از ساقها بر خلاف قاعده دیگر عمود است.
- ساقهای قائم و مایل: در ذوزنقه قائمالزاویه، ساقی که بر خلاف قاعده عمود است، ساق قائم و دیگر ساق، ساق مایل نامیده میشود.
این ویژگیها باعث میشود ذوزنقه یک شکل هندسی جالب و مورد مطالعه در ریاضیات و هندسه باشد و معمولا در مسائل مختلف به عنوان یک الگو یا مثال استفاده میشود.
محاسبه مساحت ذوزنقه
برای محاسبه مساحت ذوزنقه، میتوانید از دو روش مختلف استفاده کنید: با استفاده از اندازه دو ساق و زاوای میانی، یا با استفاده از اندازه دو ضلع غیر موازی و ارتفاع.
با استفاده از اندازه دو ضلع غیر موازی و ارتفاع: فرض کنید a و b اندازه دو ضلع غیر موازی ذوزنقه و h ارتفاع (فاصله بین دو ساق موازی) باشد.
(a + b) × h / 2 = مساحت ذوزنقه
در هر دو روش، مساحت ذوزنقه با واحد معمولاً متر مربع یا واحد دیگری که برای اندازه استفاده میکنید، محاسبه میشود. مطمئن شوید که اندازهها به همان واحد باشند تا محاسبات صحیح انجام شود.
لطفاً دقت کنید که در مثالهایی که ذوزنقه متساوی الساقین است، از روش دوم (با استفاده از اندازه ضلعها و ارتفاع) استفاده کنید، زیرا در این حالت اندازه دو ساق مساوی است.
مساحت ذوزنقه قائم الزاویه نیز بر اساس فرمول زیر به دست می آید.
۲ ÷ [(مجموع دو قاعده) × ارتفاع] = مساحت ذوزنقه
حل مثال های کاربردی مساحت ذوزنقه
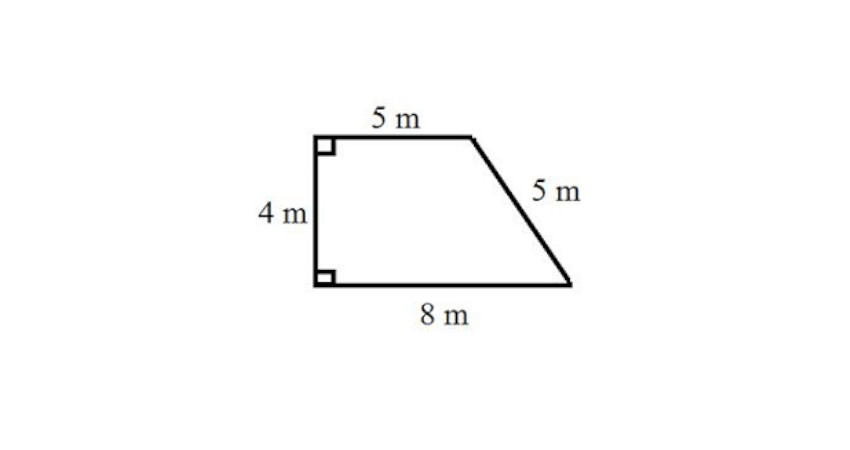
طبق تصویر قرار داده شده مساحت ذوزنقه برابر است با: 26 =۲ ÷ [(8+5) ×4] = مساحت ذوزنقه
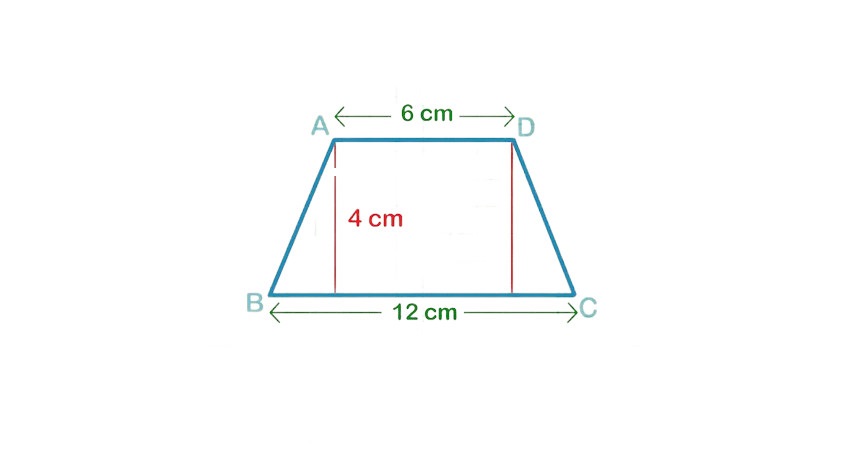
طبق تصویر قرار داده شده مساحت ذوزنقه برابر است با: 36 =(12 +6) × 4 / 2 = مساحت ذوزنقه
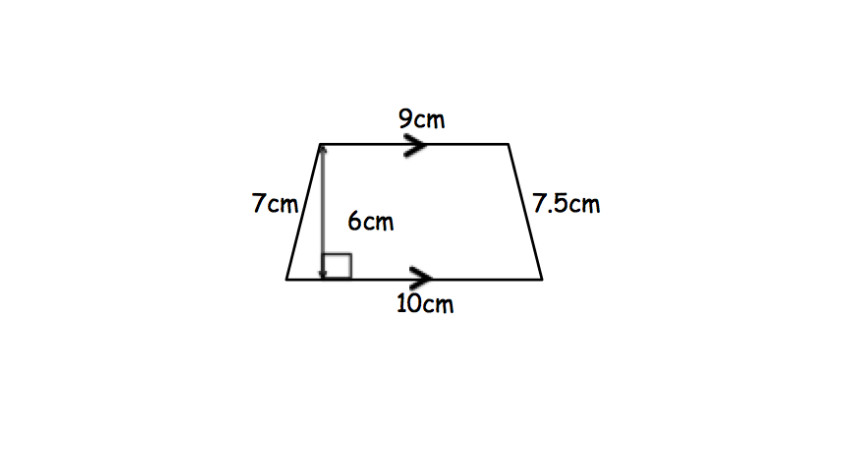
طبق تصویر قرار داده شده مساحت ذوزنقه برابر است با: 57 =(9+10) × 6/ 2 = مساحت ذوزنقه
خصوصیات بارز ذوزنقه
به طور خلاصه در ذوزنقه:
- زاویههای مجاور به هر ساق مکمل یکدیگر هستند. این به این معنا است که جمع هر زاویه مجاور به یک ساق با زاویه مجاور به ساق دیگر برابر با ۱۸۰ درجه است.
- ساقهای شکل (اضلاع غیر موازی) در ذوزنقه متساوی الساقین با هم برابر هستند. در واقع دو ساق از نوعی در ذوزنقه متساوی الساقین با طول یکسان بوده و زاویهی میان آن ها نیز برابر است.
- زاویههای مجاور به هر قاعده با هم مساوی هستند که به این معنا است که زاویهای که به یکی از قاعده متصل شده با زاویهای که به قاعده دیگر متصل شده باشد، برابر است.
- قطرها در ذوزنقه متساوی الساقین با هم مساوی هستندکه قطری که از یک راس به راس مقابل کشیده شود، برابر با قطر دیگر ذوزنقه است.
- در ذوزنقه قائمالزاویه یکی از ساقها بر هر دو قاعده عمود است، یعنی یکی از ساقها به صورت عمودی به هر دو قاعده متصل است.
- در ذوزنقه قائمالزاویه، ساق عمود بر دو قاعده ساق قائم و دیگری ساق مایل نامیده میشود که به معنا این است که ساق قائم با قاعده عمودی است و ساق مایل به قاعده افتادهای که به ساق قائم متصل نیست.
با داشتن چنین اطلاعاتی می توانید مساحت ذوزنقه های مختلف را راحت تر محاسبه کنید.
