فرمول محاسبه محیط و مساحت متوازی الاضلاع + مثال های متنوع

شاید این مطالب برایتان مفید باشد

حروف الفبا به ترتیب | شعر، جدول و آموزش

3 هفته پیش

معرفی میخکوبی و نقش آن در ساخت و ساز

3 هفته پیش

مشاوره انتخاب رشته در کنکور

7 فروردین, 1403

مسائل محیط و مساحت متوازی الأضلاع بخش مهمی از آموزش ریاضی را تشکیل می‌دهند. متوازی الأضلاع یک چند ضلعی است که دو ضلع روبروی آن با هم مساوی و موازی هستند. اندازه‌های متوازی الأضلاع در هر ابعاد بوده و می‌توان آن را در محل مربوطه مشخص کرد تا محیط و مساحت آن به طور فوری محاسبه شود. این اشکال از جنس مستطیل هستند، با این تفاوت که شکل آن‌ها از شکل اولیه‌ی خود (مستطیل) تغییر یافته است، بنابراین نحوه محاسبه محیط و مساحت آن‌ها نسبت به مستطیل متفاوت است. متوازی الاضلاع دو زاویه باز و دو زاویه تند دارد و خط تقارن و قطر یکسان‌هم ندارد، اما مرکز تقارن دارد. چند نکته مهم و قابل ذکر که باید در اینجا گفته شود. در زیر آمده است.

• قطرهای متوازی الاضلاع همدیگر را نصف می‌کنند.
• مجموع زوایای مجاور در متوازی الاضلاع مکمل هم هستند و مجموع آن ها برابر با ۱۸۰ درجه است
• هر قطر متوازی الاضلاع، آن را به دو مثلث هم‌نهشت تبدیل می‌کند

برای حل مسائل مساحت و محیط متوازی الاضلاع، بهتر است که با مهمترین بخش‌های آن بیشتر آشنا شویم.

• قاعده: قاعده معمولا ضلعی درنظر گرفته می‌شود که در قسمت پایین و کف شکل قرار دارد. در ریاضی مساحت و محیط متوازی الاضلاع، قاعده معمولا با حرف b (Base) نشان داده می‌شود.
• ارتفاع: ارتفاع خطی است که از قاعده بالای شکل بر قاعده پایین آن عمود می‌شود. در فرمول محیط متوازی الاضلاع و یا مساحت آن، ارتفاع با h (Height) نشان داده می‌شود.
• رأس: به محل برخورد دو ضلع متوازی الاضلاع قطر می‌گویند.
• قطر: قطر متوازی الاضلاع خطی است که دو رأس روبرو را به یکدیگر وصل می‌کند. متوازی الاضلاع دو قطر دارد. نماد قطر نیز d (Diameter) است.

فرمول محاسبه محیط متوازی الاضلاع

محیط یک شکل به طور کلی مجموع مسافتی که پیرامون شکل های هندسی به خط و مسیری گفته می شود که یک سطح را در بر می گیرد. محیط متوازی الاضلاع برابر جمع تمام ضلع‌های آن است. این اندازه از رابطه «مجموع دو ضلع مجاور ضربدر دو» نیز به دست می‌آید. برای محاسبه محیط متوازی‌الاضلاع باید از رابطه زیر استفاده کرد:

ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

در متوازی الاضلاع، اندازه ضلع‌های روبه‌رویی با هم برابر است. به همین دلیل می‌توانیم رابطه بالا را به صورت زیر بازنویسی کنیم:

ضلع دوم + ضلع اول + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

(ضلع دوم × 2) + (ضلع اول × 2) =

(ضلع دوم + ضلع اول) × 2 =

ضلع اول و دوم در متوازی الاضلاع بالا، در کنار یکدیگر یا اصطلاحا مجاور هستند. از این‌رو، بهتر است فرول محیط متوازی الاظلاع را به صورت زیر بنویسیم:

(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع

فرمول محیط متوازی الاضلاع برابر «عرض × 2 + طول × 2» یا «P=2a+2b» است.

۲*(مجموع دو ضلع مجاور) = محیط

محاسبه محیط متوازی الاضلاع پنجم ابتدایی = 2 × (اندازه ضلع کوچک + اندازه ضلع بزرگ)

مثال های متنوع برای محاسبه محیط متوازی الاضلاع

مثال 1: محاسبه اندازه دور متوازی الاضلاع

اندازه هر یک از ضلع‌های متوازی‌الاضلاع زیر، در کنار آن نمایش داده شده است. محیط متوازی‌الاضلاع را حساب کنید.

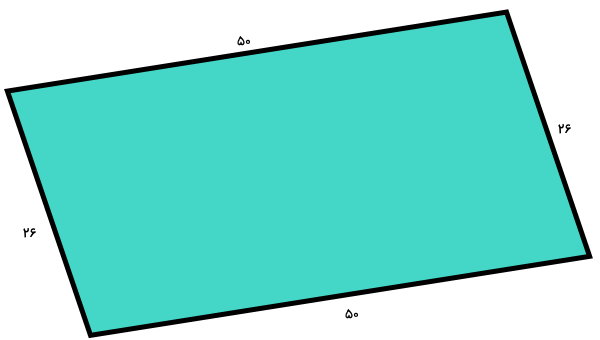
اندازه محیط متوازی‌الاضلاع بالا، از جمع چهار ضلع آن به دست می‌آید:

ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

۲۶ + ۵۰ + ۲۶ + ۵۰ = محیط متوازی الاضلاع

۱۵۲ = محیط متوازی الاضلاع

در نتیجه، محیط متوازی‌الاضلاع برابر 152 واحد طول است.

مثال 2: محاسبه محیط متوازی الاضلاع با فرمول

اندازه دو ضلع مجاور در یک متوازی‌الاضلع برابر 21 و 24 سانتی‌متر است. محیط متوازی‌الاضلاع را به دست بیاورید.

برای حل این مسئله، فرمول محیط متوازی‌الاضلاع را می‌نویسیم و اندازه‌های معلوم را درون آن قرار می‌دهیم:

(عرض × 2) + (طول × 2) = محیط متوازی‌الاضلاع

(۲۴ × 2) + (۲۱ × 2) = محیط متوازی‌الاضلاع

(۴۸) + (۴۲) = محیط متوازی‌الاضلاع

۹۰ = محیط متوازی‌الاضلاع

در نتیجه، محیط متوازی‌الاضلاع برابر ۹۰ سانتی‌متر است.

مثال 3: مثال ساده برای محاسبه محیط متوازی الاضلاع همراه فرمول

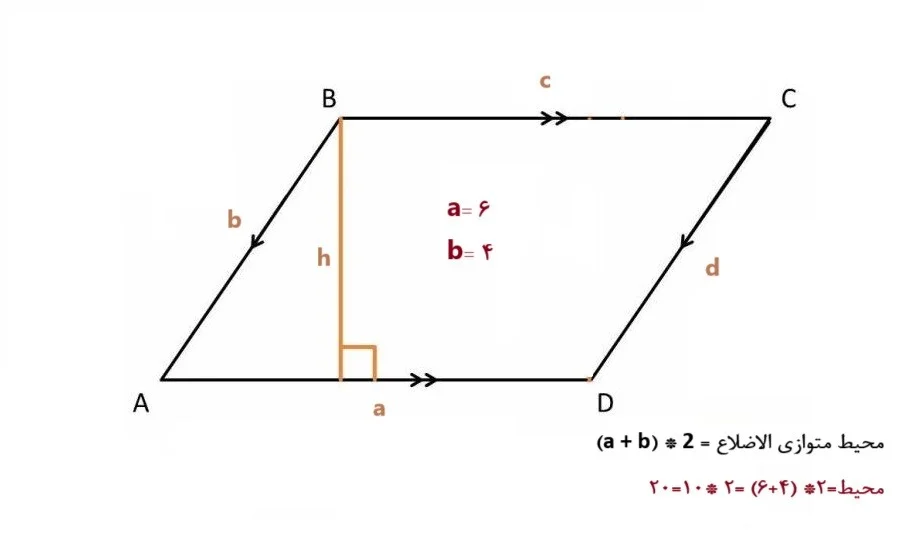
اگر یک متوازی الاضلاع دو ضلع مجاور با طول ۴ و ۶ داشته باشد، محیط آن به این صورت محاسبه می‌شود:

محیط=۲* (۴+۶) =۲ *۱۰=۲۰

پس محیط این متوازی الاضلاع برابر با ۲۰ واحد است.

مثال 4: محاسبه محیط متوازی الاضلاع به دو روش

محیط متوازی الاضلاع زیر را به دو روش حساب کنید.

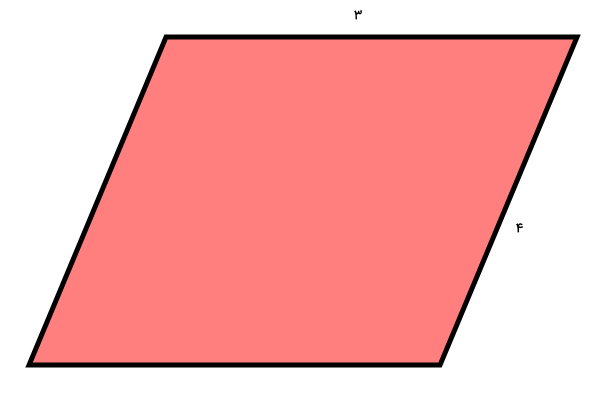
در متوازی الاضلاع بالا، فقط اندازه دو ضلع مجاور داده شده است. ضلع‌های روبه‌رویی در متوازی الاضلاع، هم‌اندازه‌اند. بنابراین، اندازه تمام ضلع‌ها را می‌دانیم.

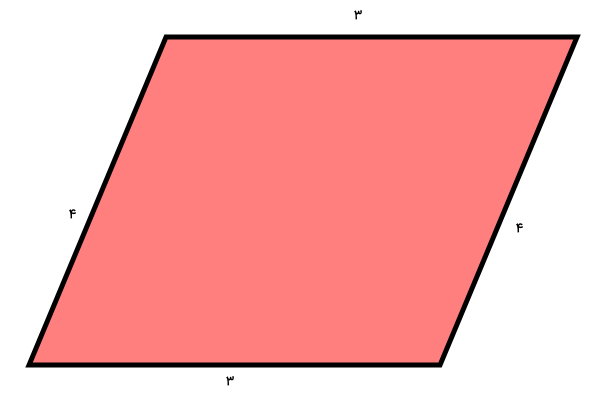
برای محاسبه محیط متوازی الاضلاع، دو روش وجود دارد. روش اول، با جمع تمام اندازه‌ها انجام می‌شود:

ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

4 + 3 + 4 + 3 =

14 =

روش دوم محاسبه محیط، استفاده از رابطه مخصوص به آن است:

(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع

(4 + 3) × 2 =

(7) × 2 =

14 =

همان‌طور که مشاهده می‌کنید، نتیجه هر دو روش برابر است.

 

محاسبه مساحت متوازی الاضلاع

مساحت متوازی الاضلاع یک محدوده و سطح یک شکل می باشد، برای محاسبه مساحت متوازی الاضاع به قاعده و ارتفاع آن نیاز دارید. برای بدست آوردن مساحت متوازی الاضلاع تنها به 2 چیز نیاز دارید که کار آسانی می باشد. اولین اندازه مورد نیاز برای شما، ارتفاع متوازی الاضلاع است و دومین عدد مورد نیاز، قاعده است. بعد از محاسبه این دو عدد که حال بستگی به مسئله دارد که آیا این اعداد را مشخص کرده باشد یا خیر! اگر مشخص شده باشد کار شما آسان می باشد و اگر مشخص نکرده باشد باید بر اساس داده های مسئله اقدام به حل کنید. اینک باید دو عدد مشخص شده را با یکدیگر ضرب کنید. برای محاسبه مساحت متوازی‌الاضلاع باید از رابطه زیر استفاده کرد:

محاسبه محیط متوازی الاضلاع پنجم ابتدایی: = 2 × (اندازه ضلع کوچک + اندازه ضلع بزرگ)

فرمول مساحت متوازی الاضلاع: «قاعده ضربدر ارتفاع» با عبارت جبری S=bh است.

فرومل مساحت متوازی الاضلاع به زبان ساده: ارتفاع × قاعده = مساحت متوازی‌الاضلاع

مثال های متنوع برای محاسبه مساحت متوازی الاضلاع

مثال 1: محاسبه مساحت متوازی الاضلاع با قاعده و ارتفاع

تصویر زیر، یک متوازی‌الاضلاع و اندازه دو ضلع مجاور آن را نمایش می‌دهد. اگر ارتفاع نظیر طول متوازی‌الاضلاع، برابر ۳ باشد، مساحت آن چقدر خواهد بود؟

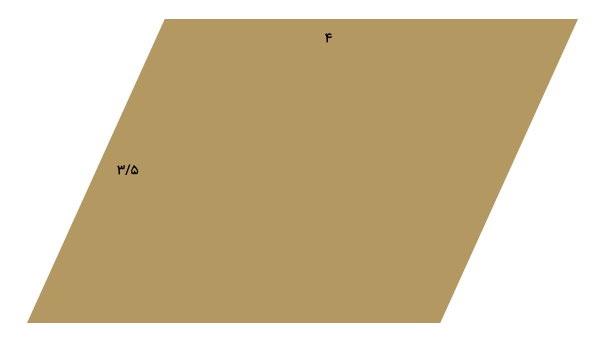
متوازی‌الاضلاع بالا، دارای دو ضلع به اندازه‌های 4 و 3/5 است. ضلع بزرگ این متوازی‌الاضلاع، به عنوان طول و ضلع کوچک آن، به عنوان عرض در نظر گرفته می‌شود. به منظور تعیین مساحت، فرمول آن را می‌نویسیم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

مطابق با صورت سوال، ارتفاع نظیر طول متوازی‌الاضلاع را داریم. این اندازه برابر ۳ است. بنابراین، به جای قاعده در فرمول بالا، باید اندازه طول متوازی‌الاضلاع، یعنی 4 را قرار دهیم:

3 × 4 = مساحت متوازی‌الاضلاع

۱۲ = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 12 واحد سطح است. واحد سطح، معمولا به صورت طول مربع (سانتی‌متر مربع، متر مربع، اینچ مربع و غیره) بیان می‌شود.

مثال 2: محاسبه مساحت متوازی الاضلاع به صورت جبری

مساحت متوازی‌الاضلاعی زیر را حساب کنید.

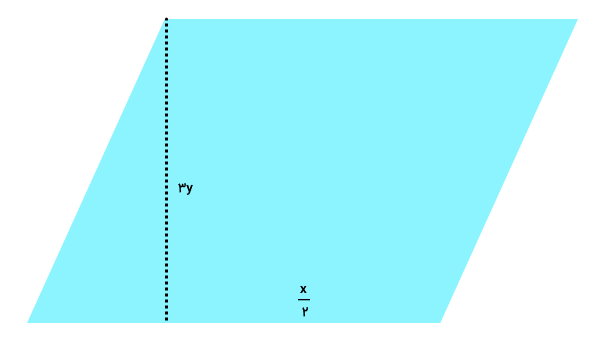
برای حل این مثال، فرمول مساحت متوازی الاضلاع به صورت جبری را می‌نویسیم:

$$S=bh$$

• S: مساحت متوازی‌الاضلاع
• b: قاعده متوازی‌الاضلاع
• h: ارتفاع نظیر قاعده

اکنون، اندازه‌های داده شده را درون فرمول بالا قرار می‌دهیم:

$$S=\frac{x}{۲}\times ۳y$$

$$S=\frac{۳}{۲}xy$$

مساحت متوازی‌الاضلاع به صورت جبری به دست آمد.

مثال 3: مثالی ساده برای محاسبه مساحت متوازی الاضلاع

ارتفاع یک متوازی الاضلاع برابر 41 سانتی‌متر و قاعده آن برابر 100 سانتی‌متر است. مساحت متوازی الاضلاع را به دست بیاورید.

 

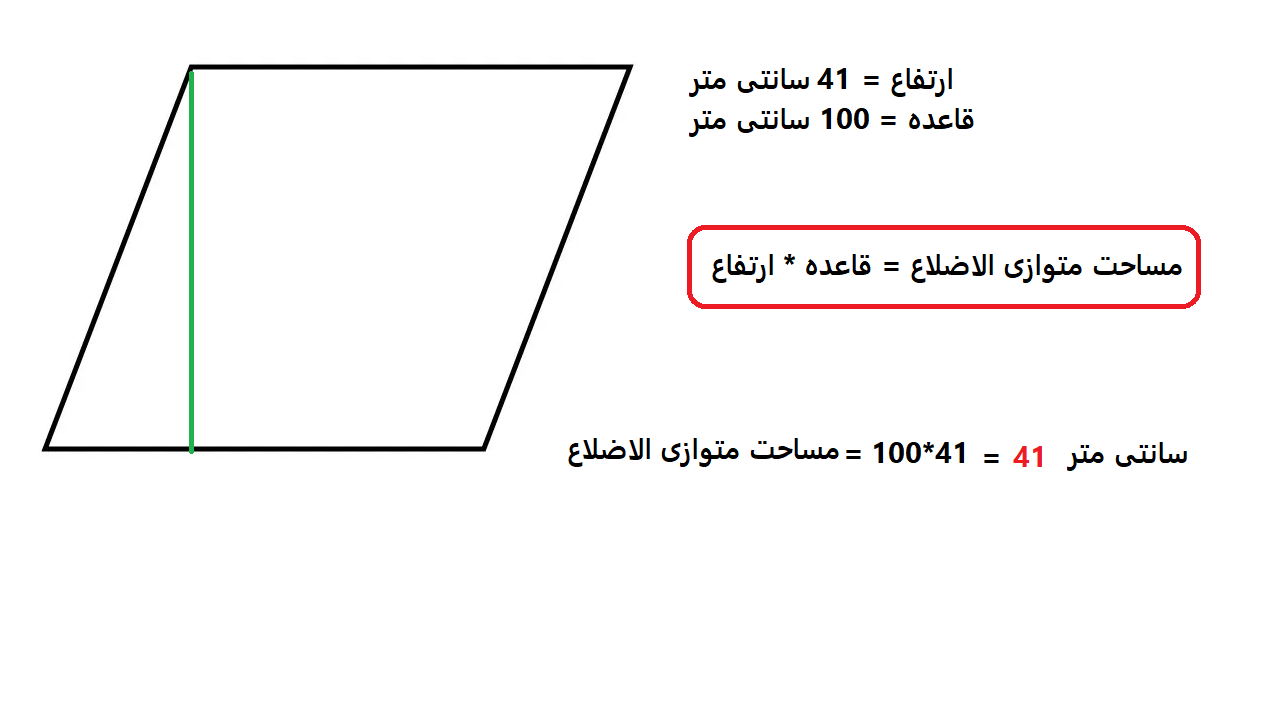مثال 4: برای محاسبه مساحت متوازی اضلاع

مساحت شکل زیر چند است؟ (اندازه‌های نمایش داده شده به میلی‌متر هستند.)

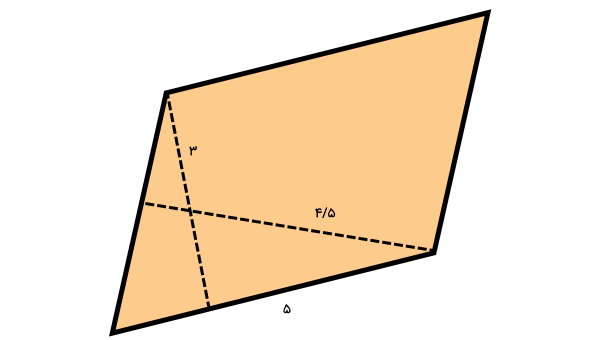
اندازه یک ضلع و دو ارتفاع متوازی‌الاضلاع را داریم. مساحت متوازی‌الاضلاع، با ضرب قاعده در ارتفاع نظیر محاسبه می‌شود. بر اساس شکل بالا، ارتفاع نظیر قاعده 5 میلی‌متری برابر 3 میلی‌متر است. بنابراین، مساحت متوازی‌الاضلاع از رابطه زیر به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۳ × ۵ = مساحت متوازی‌الاضلاع

۱۵ = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 15 میلی‌متر مربع است.

مثال 5: برای محاسبه مساحت متوازی اضلاع

مساحت شکل زیر به دست آورید. (اندازه‌های نمایش داده شده به سانتی‌متر هستند.)

شکل بالا، متوازی‌الاضلاعی به قاعده 8 سانتی‌متر و ارتفاع 4 سانتی‌متر را نمایش می‌دهد. بر اساس فرمول مساحت متوازی‌الاضلاع داریم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

اندازه ارتفاع و قاعده را درون فرمول قرار می‌دهیم و آن‌ها را در هم ضرب می‌کنیم:

۴ × ۸ = مساحت متوازی‌الاضلاع

32 = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر ۳۲ سانتی‌متر مربع است.