دانشنامه سیب دانشنامه سیب ! دکوراسیون داخلی، پزشکی و زندگی روزمره
شاید این مطالب برایتان مفید باشد
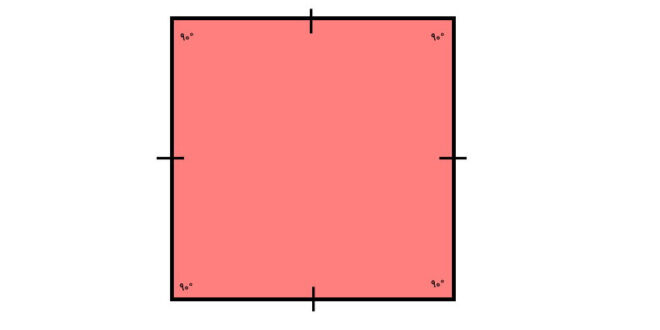
مربع یک نوع ویژه از چهارضلعی است که تمام زوایا و ضلع‌های آن به طول یکسان معروفند. ویژگی‌های اصلی مربع به شرح زیر است:
- زوایا: همه‌ی زوایا در یک مربع ۹۰ درجه هستند، به این معنا که همه‌ی زاویه‌های آن قائمه (عمودی) هستند.
- ضلع‌ها: تمام ضلع‌های یک مربع به طول یکسان هستند.
- مقابلت ضلع‌ها: ضلع‌های مقابل یک مربع موازی هم هستند.
- قطرهای مربع: قطرهای یک مربع برابرند و از مرکز به دو گوشه‌ی مقابل از آن می‌رسند. قطرهای مربع نیز مساوی یکدیگر هستند و به ازای هر قطر، دو مثلث قائم‌الزاویه‌ی همانندی ایجاد می‌کنند.
مربع‌ها در مختلف زمینه‌های هندسی، مهندسی، فیزیک و بسیاری از موارد دیگر به کار می‌روند. آن ها به عنوان شکل‌های پایه‌ای در طراحی و تجزیه و تحلیل ساختارها و الگوها به کار می‌روند و خواص منحصر به فردشان باعث شده تا به عنوان ابزاری مهم در حل مسائل مختلف استفاده شوند.
مساحت مربع چیست؟
مساحت به مفهوم عمومی، میزان فضا یا پهنایی که یک شکل یا سطح در بر دارد، را نشان می‌دهد. مفهوم مساحت در ریاضیات و هندسه معمولا به معنای مقدار عددی است که به واحد مربع اندازه‌گیری می‌شود. مساحت مربع برابر است با طول یک ضلع آن به توان 2، زیرا هر مربعی یک مستطیل است و با ضرب طول و عرض آن در هم مساحتش بدست می آید. مساحت مربع در مختلف زمینه‌ها کاربرد دارد. در مهندسی، معماری، فیزیک، و حتی کشاورزی، مفهوم مساحت به عنوان معیاری اساسی جهت اندازه‌گیری و تحلیل فضاها و سطوح مورد استفاده قرار می‌گیرد، همچنین در مسائل محاسباتی و تئوری اعداد، مفاهیم مربوط به مساحت مربع نقش مهمی ایفا می‌کنند
مساحت مربع چگونه به دست می آید؟
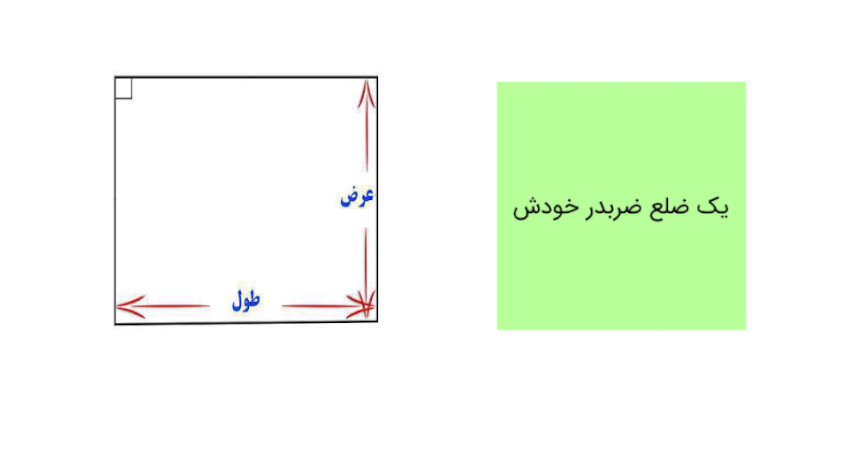
مساحت مربع برابر با ضرب طول یکی از ضلع‌های آن در خودش است. در واقع با توجه به این که تمام ضلع‌های یک مربع به طول یکسان هستند، می‌توان مساحت مربع را به سادگی با استفاده از فرمول زیر محاسبه کرد:
مساحت مربع = طول ضلع × طول ضلع
این فرمول به عنوان یک اصول پایه‌ای در محاسبه مساحت مربع استفاده می‌شود. به عبارت دیگر، مساحت مربع برابر با مربع طول یک ضلع آن است. اگر طول ضلع مربع به واحد متر باشد، مساحت آن به واحد متر مربع خواهد بود.
حل مثال های کاربردی
برای درک مساحت مربع مثال های کاربردی را برایتان حل کرده ایم تا بتوانید با هر ضلع مربعی مساحت آن را به دست آورید.
با توجه به شکل های بالا مساحت مربع ها به صورت زیر محاسبه می شود:
- مساحت مربع با ضلع 3 سانتی متر مربع برابر است با: 9 = 3 ×3
- مساحت مربع با ضلع 6 سانتی متر مربع برابر است با: 36 = 6 ×6
- مساحت مربع با ضلع 7 سانتی متر مربع برابر است با: 49 = 7 ×7
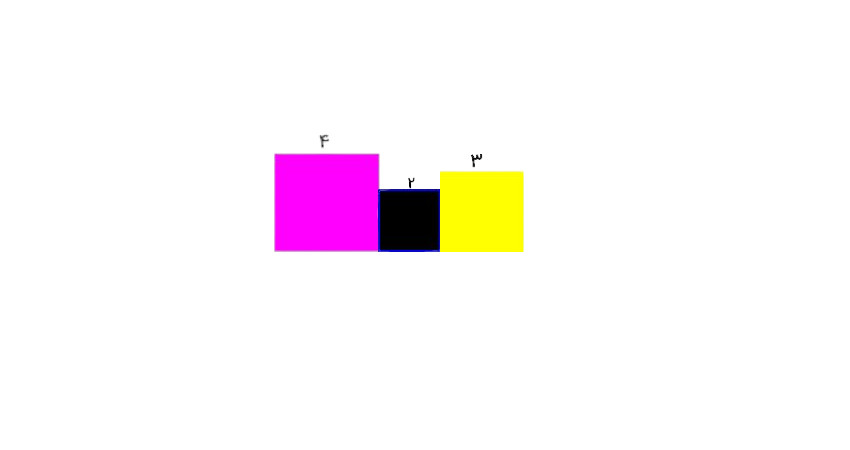
برای سخت شدن موضوع یک مثال راحت برای به دست آوردن مساحت کل شکل بالا را قرار داده ایم در این شکل مساحت کل به صورت زیر محاسبه می شود:
- مساحت مربع با ضلع 3 سانتی متر مربع برابر است با: 9 = 3 ×3
- مساحت مربع با ضلع 2 سانتی متر مربع برابر است با: 4 = 2×2
- مساحت مربع با ضلع 4 سانتی متر مربع برابر است با: 16 = 4 ×4
- مساحت کل مربع ها برابر است با: 29=9+4+16
با توجه به مثال های بالا به راحت بودن به دست آوردن مساحت مربع پی بردید، پس می توانید مساحت مربع با هر اندازه ای را به دست آورید.
مساحت مربع با قطر
برای اندازه گیری مساحت مربع با قطر، فرمول آن به شکل دیگری عنوان می شود، این فرمول عبارت اند از:
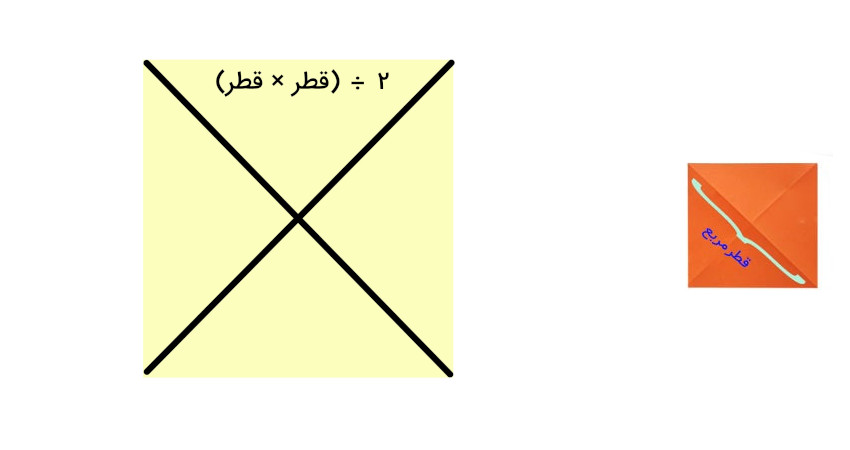
2 ÷ (قطر × قطر) = مساحت مربع
برای درک موضوع چند مثال برایتان قرار داده ایم
مساحت مربعی با قطر 4 سانتی متر برابر است با: 8= 2 ÷ (4 × 4)
مساحت مربعی با قطر 8 سانتی متر برابر است با: 32= 2 ÷ (8 ×8)
نسبت مساحت مربع‌های متشابه
اگر دو مربع متشابه باشند و ضلع یکی از آن‌ها به طول a و ضلع مربع دیگر به طول b باشد و باشد، آنگاه نسبت مساحت مربع اول به مربع دوم به شکل زیر تعریف می‌شود:
مساحت مربع دوم مساحت مربع اول = نسبت مساحت
این نسبت، نمایانگر نسبت مساحت دو مربع متشابه است. اگر نسبت مساحت بزرگتر از ۱ باشد، به این معناست که مربع اول بزرگتر از مربع دوم است. اگر نسبت مساحت برابر با ۱ باشد، به این معناست که مربع‌ها هم‌اندازه‌اند. اگر نسبت مساحت کوچکتر از ۱ باشد، به این معناست که مربع اول کوچکتر از مربع دوم است. نسبت مساحت مربع‌های متشابه یک مفهوم مهم در هندسه و محاسبات است که در مسائل مختلف مانند مقایسه اندازه‌ها و تغییرات مقیاسی به کار می‌رود.
